最近玩了一下今年Science上发表的一篇关于聚类的文章。记录一下。
算法的过程并不复杂,但确实十分聪明。算法的输入只需要一个distance的矩阵,第i行第j列的元素就是第i个数据和第j个数据的距离。
文章首先定义了一个数据的密度(density):
其中:
在作者的给出的代码里对密度的定义给出了一个更合理的公式:
简单的来说,这两个公式都反映了一个数据其一个小邻域内的其他数据的多少或者稠密程度,也就估计出来了这个数据的一个局部的密度。
值得一提的是dc这个值,对算法的影响还是比较大,文章里给出的建议是升序排列distance,然后取1%到2%的那个distance作为dc。
然后需要计算delta:
这个值越高意味着这个数据越有可能是聚类的中心,因为delta值是这个数据与比自己的密度更大的数据之间最小的距离,这个距离越大,说明这个数据远离了其他比自己密度大的数据,是自己的邻域里的局部最大,也就是题目中说的density peaks。
当然在保证这个数据有很大的delta值的情况下,也需要保证这个数据有很高的density,否则就意味着这个数据是一个噪声,因为它既远离了其他的高密度区域,自己也不处于一个高密度区域(很小的density值)。
在作者给出的matlab版本的代码里,在计算完了密度和delta之后,画出了横轴为密度,纵轴为delta的decision graph,然后可以认为选定一个点来决定最小的delta值和密度值,在dc选择合理的情况下,通常可以很轻松地作出这个决定。如下图:
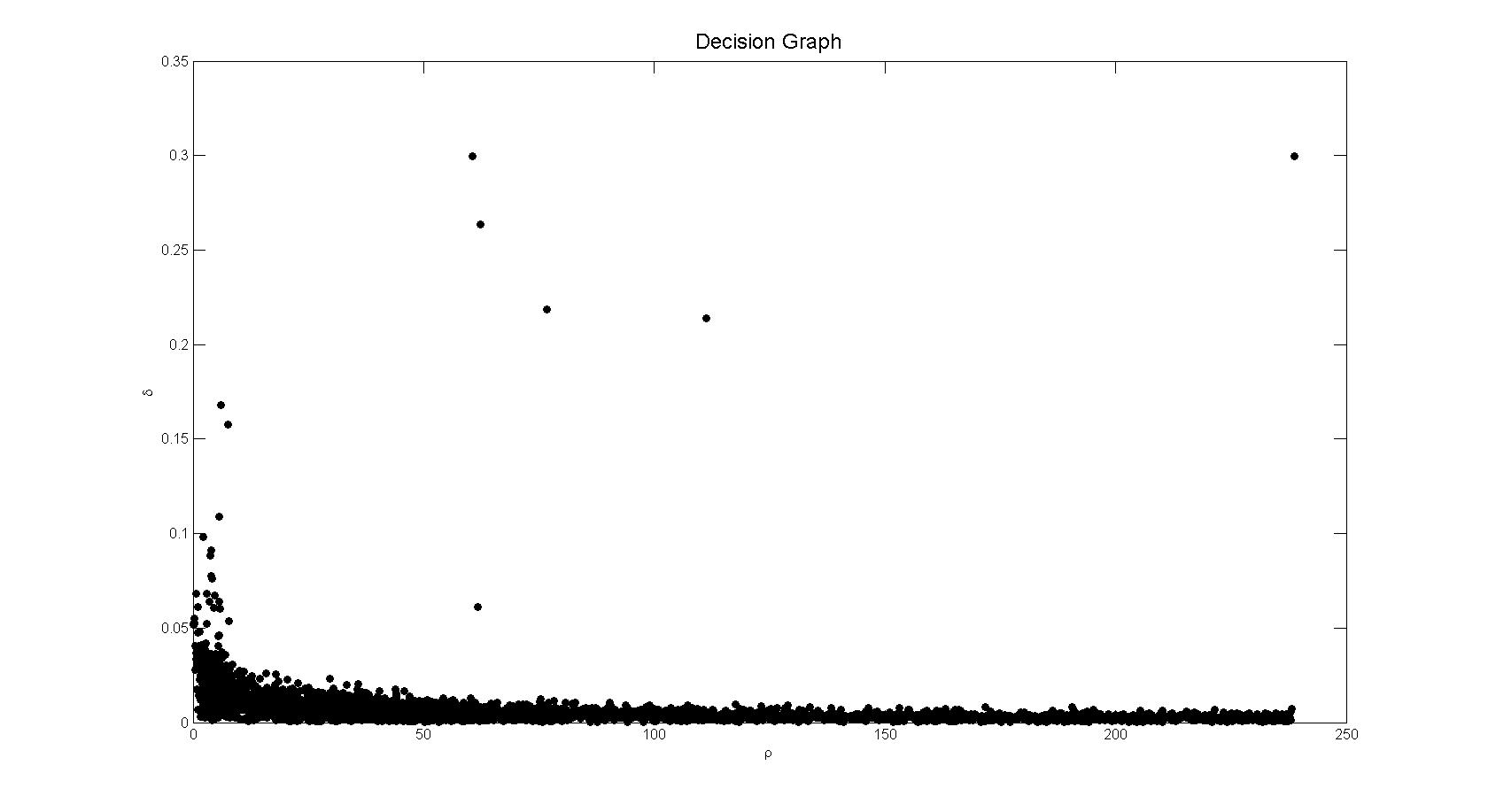
接下来需要对除了聚类中心的数据进行指派类别,第i个数据的类别和比它有更高密度的子集里的最近邻的那个数据的类别一样,通过这种扩散的方法,类别的指派从各个聚类中心(也是各个类的density peak)向低密度的区域指派。通常的聚类方法比如kmeans,指派的时候,只是简单的将数据指派到距离最近的那个中心,但是如果数据的分布本身不是球形的,而是椭圆甚至某种奇怪的曲线的话,这样的指派显然是错误的。
但是如果按照本文的方法,就可以保证数据的真实分布被反映出来。还有一个优点就是类别的指派过程是单步的,不像kmeans等聚类方法需要迭代。
然后就是最后一个步骤,找到halo区域,并且定义为噪声。首先对每一个类定义一个border region,这个区域是属于这个类别而且有距离其他类别数据小于dc的数据,这些数据会出现在各个类别的交界区域。然后将这个区域内最大的密度定义为$\rho_{b}$。
在这个类当中,所有密度比$\rho_{b}$小的数据都被定义为噪声。这样假设的合理性在于,和其他类的交界区域已经是这个类比较低密度的区域,如果比这个密度还要低,说明这些数据已经远离了这个类的核心区域,理应被定为噪声。作者提供的测试数据得到的结果见下图:
总结一下,这个算法的核心思想在于定义了密度,我的体会是这个密度在数据量比较充足的情况下,和数据本身的真实的概率分布很接近,也就是说,用这个算法,不论去估计什么样形式的数据分布(高斯、多项式、卡方,甚至自定义的)都依靠数据估计得到比较准确的密度值,而不是去对数据的分布预先做出假设。但这也带来了一个隐患,在实际的模式识别问题中,我们面对的数据分布通常是高维的,很多时候也是不充足的,通过这个方法估计得到的密度值也就可能不够准确。
另外,数据充足与否是一个相对的概念,不是说有一万个数据就比一千个数据充足,如果一千个数据的那个分布比较简单,且数据都靠近分布的核心区域,比较稠密,那也是充足的;一万个数据,但是如果数据分布很复杂,变化很多,这一万个数据又比较分散,也可以认为这一万个数据是不充足的。
最近还在用这个算法做更多的实验,有新的结果之后会保持更新。
再另外,作者主页提供的matlab代码运行效率实在太慢,我自己实现了一个稍微快一些的版本,可以看这里: